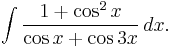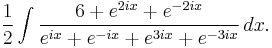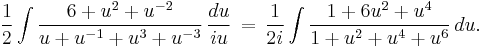Integration using Euler's formula
In integral calculus, complex numbers and Euler's formula may be used to evaluate integrals involving trigonometric functions. Using Euler's formula, any trigonometric function may be written in terms of eix and e−ix, and then integrated. This technique is often simpler and faster than using trigonometric identities or integration by parts, and is sufficiently powerful to integrate any rational expression involving trigonometric functions.
Contents |
Euler's formula
Euler's formula states that
Substituting −x for x gives the equation
These two equations can be solved for the sine and cosine:
Simple example
Consider the integral
The standard approach to this integral is to use a half-angle formula to simplify the integrand. We shall use Euler's identity instead:
At this point, it would be possible to change back to real numbers using the formula e2ix + e−2ix = 2 cos 2x. Alternatively, we can integrate the complex exponentials and not change back to trigonometric functions until the end:
Second example
Consider the integral
This integral would be extremely tedious to solve using trigonometric identities, but using Euler's identity makes it relatively painless:
At this point we can either integrate directly, or we can first change the integrand to cos 6x - 2 cos 4x + cos 2x and continue from there. Either method gives
Using real parts
In addition to Euler's identity, it can be helpful to make judicious use of the real parts of complex expressions. For example, consider the integral
Since cos x is the real part of eix, we know that
The integral on the right is easy to evaluate:
Thus:
Rational expressions
In general, this technique may be used to evaluate any rational expression involving trigonometric functions. For example, consider the integral
Using Euler's identity, this integral becomes
If we now make the substitution u = eix, the result is the integral of a rational function:
Any rational function is integrable (using, for example, partial fractions), and therefore any rational expression involving trigonometric functions may be integrated as well.
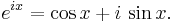
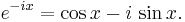
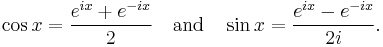
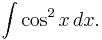
![\begin{align}
\int \cos^2 x \, dx \,&=\, \int \left(\frac{e^{ix}%2Be^{-ix}}{2}\right)^2 dx \\[6pt]
&=\, \frac{1}{4}\int \left( e^{2ix} %2B 2 %2B e^{-2ix} \right) dx
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/2b3f1ab62b435656c54fbffd3f078a8f.png)
![\begin{align}
\frac{1}{4}\int \left( e^{2ix} %2B 2 %2B e^{-2ix} \right) dx
\,&=\, \frac{1}{4}\left(\frac{e^{2ix}}{2i} %2B 2x - \frac{e^{-2ix}}{2i}\right)%2BC \\[6pt]
&=\, \frac{1}{4}\left(2x %2B \sin 2x\right) %2BC.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/2c1ae022cef875bd51ca2a4d5f69a358.png)
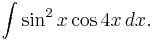
![\begin{align}
\int \sin^2 x \cos 4x \, dx \,
&=\, \int \left(\frac{e^{ix}-e^{-ix}}{2i}\right)^2\left(\frac{e^{4ix}%2Be^{-4ix}}{2}\right) dx \\[6pt]
&=\, -\frac{1}{8}\int \left(e^{2ix} - 2 %2B e^{-2ix}\right)\left(e^{4ix}%2Be^{-4ix}\right) dx \\[6pt]
&=\, -\frac{1}{8}\int \left(e^{6ix} - 2e^{4ix} %2B e^{2ix} %2B e^{-2ix} - 2e^{-4ix} %2B e^{-6ix}\right) dx.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/d48f8d10ddf6d29fa3ccd8807e31c5dc.png)
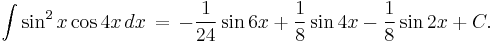
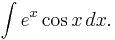
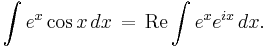
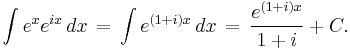
![\begin{align}
\int e^x \cos x \, dx \,&=\, \operatorname{Re}\left\{\frac{e^{(1%2Bi)x}}{1%2Bi}\right\} %2B C \\[6pt]
&=\, e^x\operatorname{Re}\left\{\frac{e^{ix}}{1%2Bi}\right\} %2BC \\[6pt]
&=\, e^x\operatorname{Re}\left\{\frac{e^{ix}(1-i)}{2}\right\} %2BC \\[6pt]
&=\, e^x\,\frac{\cos x %2B \sin x}{2} %2BC.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/fe0f376e580143ffd886fffdc23ea40a.png)